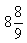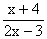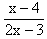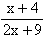| 1. | Dari ramalan cuaca kota-kota besar di dunia tercatat suhu tertinggi dan terendah adalah sebagai berikut : Moskow : terendah -5�C dan tertinggi 18�C; Mexico : terendah 17�C dan tertinggi 34�C; Paris : terendah -3�C dan tertinggi 17�C; Tokyo : terendah -2�C dan tertinggi 25�C. Perubahan suhu terbesar terjadi di kota ........ | ||||||||||
|
| 2. | Ibu membeli 40 kg gula pasir. Gula itu akan dijual eceran dengan dibungkus plastik masing-masing beratnya 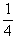 kg. Banyak kantong plastik berisi gula yang dihasilkan adalah........ kg. Banyak kantong plastik berisi gula yang dihasilkan adalah........ | ||||||||||
|
| 3. | 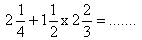 | ||||||||||
|
| 4. | Untuk membuat 60 pasang pakaian, seorang penjahit memerlukan waktu selama 18 hari. Jika penjahit tersebut bekerja selama 24 hari, berapa pasang pakaian yang dapat dibuat........ | ||||||||||
|
| 5. | Sebungkus coklat akan dibagikan kepada 24 anak, setiap anak mendapat 8 coklat. Jika coklat itu dibagikan kepada 16 anak, maka banyak coklat yang diperoleh setiap anak adalah ........ | ||||||||||
|
| 6. | Andi membeli 10 pasang sepatu seharga Rp 400.000,00, kemudian dijual secara eceran. Sebanyak 7 pasang sepatu dijual dengan harga Rp 50.000,00 per pasang, 2 pasang dijual Rp 40.000,00 per pasang, dan sisanya disumbangkan. Persentase keuntungan yang diperoleh Andi adalah ........ | ||||||||||
|
| 7. | Pada tumpukan batu bata, banyak batu bata paling atas ada 8 buah, tepat di bawahnya ada 10 buah, dan seterusnya setiap tumpukan di bawahnya selalu lebih banyak 2 buah dari tumpukan di atasnya. Jika ada 15 tumpukan batu bata (dari atas sampai bawah), berapa banyak batu bata pada tumpukan paling bawah ........ | ||||||||||
|
| 8. | Penyelesaian dari pertidaksamaan 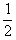 (2x - 6) (2x - 6)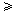 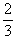 (x - 4) adalah ........ (x - 4) adalah ........ | ||||||||||
|
| 9. | Hasil dari (2x - 2) (x + 5) adalah ........ | ||||||||||
|
| 10. | 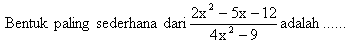 | ||||||||||
|
| 11. | Dari 40 siswa di kelas 3A, 19 orang menyukai matematika, 24 orang menyukai bahasa Inggris, serta 15 orang menyukai matematika dan bahasa Inggris. Berapa banyak siswa yang tidak menyukai matematika maupun bahasa Inggris ........ | ||||||||||
|
| 12. | Perhatikan diagram berikut ini !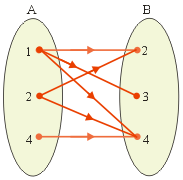 Relasi dari himpunan A ke himpunan B adalah ........ | ||||||||||
|
| 13. | Perhatikan grafik dibawah ini !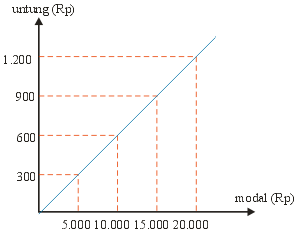 Dengan modal Rp 25.000,00, berapakah untung yang diperoleh ........ | ||||||||||
|
| 14. | Diketahui sistem persamaan 3x + 3y = 3 dan 2x - 4y = 14. Nilai dari 4x - 3y = ........ | ||||||||||
|
| 15. | Harga dua baju dan satu kaos Rp 170.000,00, sedangkan harga satu baju dan tiga kaos Rp 185.000,00. Harga tiga baju dan dua kaos adalah ........ | ||||||||||
|
| 16. | Persamaan garis yang sejajar dengan garis 2x + 3y + 6 = 0 dan melalui titik (-2, 5) adalah ........ | ||||||||||
|
| 17. | Perhatikan gambar berikut !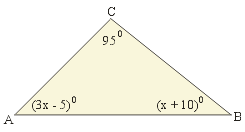 Besar sudut BAC adalah ........ | ||||||||||
|
| 18. | 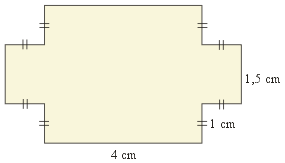 Keliling bangun di atas adalah ........ | ||||||||||
|
| 19. | Diketahui dua buah lingkaran dengan pusat A dan B, dengan panjang jari-jari masing-masing 7 cm dan 2 cm. Jika jarak AB = 13 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah ........ | ||||||||||
|
| 20. | Perhatikan gambar !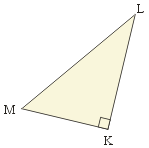 Pernyataan-pernyataan berikut yang merupakan teorema Phytagoras adalah ........ | ||||||||||
|